This distribution is usually explained with the example of tossing a coin. But we can equally think of the wildcat success ratio in an area. How many times will heads come up in a number of trials. The probability of heads for an "honest" coin is 0.5. In two throws, we expect to see one head and one tail. In reality there is variation in the number of heads seen in repeated experiments. The variation is described by the discrete binomial distribution:
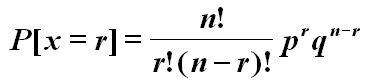
where p is the probability of a success (heads) and q = 1-p the probability of tails.
The above is the probability mass function (pmf) that gives the frequency of occurrence for each particular number of "successes" r in n repeated experiments (throws of the coin). Note that the ratio r/n is a probability that is constant and known in these repeated experiments. The variable is the number of successes.
The distribution function (cdf) is given by:
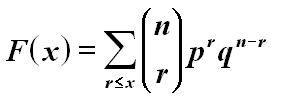
Important parameters are:
The distribution is symmetric if r/n = 0.5, but is skewed if r/n deviates from 0.5. If n is very large and r/n not too different from 0.5, the distribution (pmf) becomes smooth and can be approximated by the normal distribution with the mean and variance as given above.
In exploration we do not know the success ratio, until the area has been explored to the hilt. Then the final probability r/n is an unknown and we have to estimate the success ratio from the observed success ratio so far. That process is related to the use of the beta distribution.In the course of exploration of a larger area or basin, the success rate is not a constant. Various behaviours are found in different basins. The most common one is that the mean (success rate) is declining slowly with time. In other cases the decline is compensated by improvement of exploration techniques, notably seismic methods. Still other basins show a logistic curve for the success ratio, i.e. first a slow increase up to a maximum success rate that then later declines again See the page on creaming.