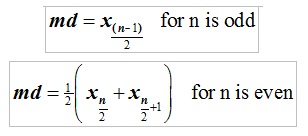Distribution Parameters
The parameters of a probability distribution which are most commonly used are:
- Measures of Location
- Measures of Dispersion
- Variance
- Standard deviation
- Variation coefficient
- Standard deviation of the Mean
- Percentiles (fractiles)
As analysis is often plagued with small samples, the parameter estimates from such samples are not always reliable, especially in the case that the assumptions underlying the formulas listed below, are violated, for instance in the case of ill-defined, or unkown distributions . Then it is useful to apply non-parametric estimation such as the Jackknife or Bootstrap methods.
Measures of Location
The mean (expectation)
The mean is the average of all the values in a sample or distribution of a variable. Hence the sum of all the values, divided by their number (sample size). Although the mean is the "mathematical expectation", ironically, you do not expect to hit the expectation during sampling!
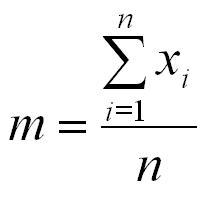
The character "m" is often used when the mean refers to the mean of a sample, while for the theoretical distribution it is denoted as "µ" or, for a variable x as x with a bar above the letter.
See also "Swansons' 30-40-30 rule" for estimating the mean from percentiles.
In many situations the mean is required, but not all values of a variable should be included in the mean. A good example is a porosity estimate. A log will give a set of porosity values, but all below a cutoff porosity are actually irrelevant, as a low porosity will be associated with a low permeability and lack of productivity. Therefore a "conditional mean" is a parameter that can be used in further analysis. A condition will lower the sample size and also affect the shape of the distribution.
In some researchers suggest that the median is easier to estimate subjectively than the mean or mode. In probabilistic reserve estimation it is the 50%-tile or P50.
This mean is relevant to the lognormal distribution. The antilog of the mean, calculated from the log-values, is the geometric mean. This is usually smaller than the linear mean of the lognormal data.
Conditional Mean
Another important example is the Mean Success Volume or MSV, the conditional mean of possible outcomes above a certain size, i.e. zero or a cutoff volume.
The median is a useful measure when e.g. the resources of a whole country are being assessed. Then there are two advantages: (1) the mean may be misleading in a skew distribution, while the median will be less affected by the skewness, and (2) there may be no good reason to add resource estimates together, if they are already the result of some probabilistic addition scheme for a vast area, or even global. The USGS used to report median estimates for the global oil and gas reserves.
The Mode
The mode is the most likely value in a sample or for a pdf. It is the top of the pdf, if there is only one top. It is also the parameter that people will give subjectively when asked for a number. If the type of distribution is not known, there is no easy formula for the calculation of the mode, but iterative procedures have been developed to locate it approximately. Distributions with more tyhan one mode are called "polymodal: .
For a normal distribution the mode coincides with the mean and the median. For a lognormal a formula is available.
A simple, but rough method is fitting a triangular distribution to the data.
The Geometric Mean
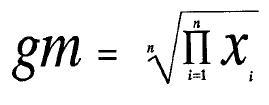
Highest Density Region ("HDR")
This related to the mode. The percentage of data that should be contained in the HDR must be specified, such as 25%. Then an iterative procedure goes through a sorted vector of the values to find the HDR.
Measures of Dispersion
The Variance
An "average" such as the mean, median or mode is a useful but insufficient description of a sample. The variation of numbers around the measure of central tendency is also very important. This spread, or dispersion can again be described by various statistical parameters. The most commonly used and useful measure is the "variance". It measures the degree of variation of individual observations with regard to the mean. It gives a weight to the larger deviations from the mean because it uses the squares of these deviations. A mathematical convenience of this is that the variance is always positive, as squares are always positive (or zero). The variance is often denoted as "var" or "sigma-square":
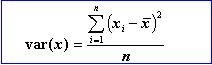
In the above formula the x with a bar on top is the mean of the observations. It has been found that in the case of a small sample a better estimate of the "population" variance can be obtained by dividing by (n-1) instead of by n.
The variance is a measure of uncertainty. As prospect appraisal tries to quantify the uncertainty of the hydrocarbon volumes that we hope to find, the variance is a fundamental concept that will appear in many of the discussions of appraisal and calibration methods. An interesting concept is "amount of information" in a statistical sense. Some statisticians use the reciprocal of the variance as such. In multivariate analysis the importance of geological variables for estimating probabilities of success and volumes is often judged on the basis of how much of the total variance they are able to explain.
The Standard Deviation
The square root of the variance is the standard deviation. It is an easier measure of dispersion as it is expressed in the same units as the observations. The standard deviation of the population is indicated by the Greek symbol sigma.
For a sample only the estimate or sx is available. The formula for a sample of size n is:
>
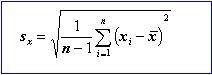
See more about the standard deviation.
Sometimes it is desirable to compare dispersion of different samples with different means. In such case the variation coefficient, defined as the standard deviation divided by the absolute value of the mean can be useful. The absolute value of the mean ensures that this dimensionless, relative measure of dispersion is always non-negative.
The mean of a finite sample is itself subject to uncertainty, except if the variable has a variance of zero. It can be shown that the standard deviation of the mean is inversely proportional to the square root of the samplesize:
Variation coefficient
Standard deviation of the mean
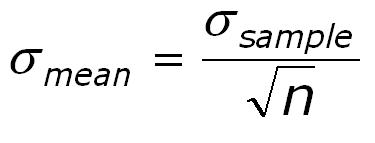
This parameter is of special interest for prospect appraisal. To illustrate this we take porosity. Usually a set of porosity data are available within a reservoir section. For a reserves calculation the mean porosity would be required. From the set of data the mean can be computed (after discarding porosities below cutoff). The uncertainty about this mean porosity input is the uncertainty of the mean, not the range derived from the standard deviation of the measured porosity data. The same logic holds a.o. for HC saturation.
Percentiles
A percentile PX is the value of the variable at which the chance of being less then or equal to the value is P percent (also called "fractiles"). So percentiles are points on the cumulative distribution curve. However, with expectation curves the situation is the reverse: PX is the value where the chance to be exceeded is equal to P. The latter is the most common way of indicating the uncertainty of the estimate. Often the P90 (proven), P50 (probable) and P10 (possible) are reported for unrisked prospective resources, but also for reserve estimates:
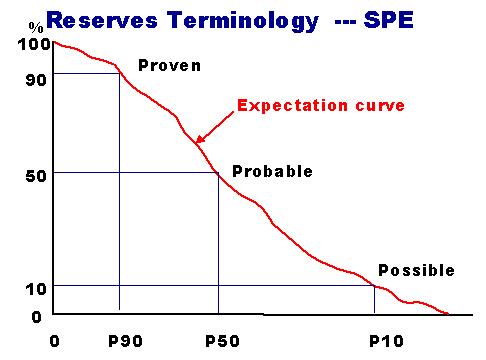
The P50 is the value that is equally likely to be exceeded than not, in other words the median. It is also often called "best estimate", although I would prefer that to be the mode, the most likely value.
It should also be noted that aggregation of distributions is preferably done by probabilistic methods, as straight addition of percentiles is rarely warranted, only if the distributions to be added are completely dependent. For the case of independence, the percentiles of different prospects can not be added. Only a
Monte Carlo analysis can make the addition, after which the percentiles in the sum-distribution can be determined.
It is customary in the oil industry to present the percentiles of the "unrisked volume" distribution, or an expectation curve of the same. That curve starts at the left at the 100% probability. The Probability of success (POS) is then separately given. See the usual classification of reserves/resources of the SPE. In this way an economic evaluation can be made for the success case. The result is then combined with the POS in the calculation of the Expected Monetary Value. In the case of the emv calculation, the unrisked, or conditional distribution of volumes starts at some economic cutoff value.