Jacknife and Bootstrap
Parameters of the petroleum system are estimated subjectively, or with the help of analogons, or even data bases. This involves investigating the type of distribution as well as estimating a number of distribution parameters. The uncertainty of a variable, such as porosity, is usually expressed as the standard deviation. For small samples the estimated standard deviation is itself uncertain. The usual approach to estimate the uncertainty of a distribution parameter is to use a known formula, such as the stdev of stdev = sdev/sqrt(2*n) where n is the sample size. here two methods are briefly discussed that are non-parametric resampling plans to obtain "standard error" of a parameter. With limited samples, a parameter is, fot instance, the variance as a measure of uncertainty and only an estimate. If we know the underlying distribution of the data, confidence ranges can be calculated to indicate how reliable the estimated variance, or other statistical measures from the sample. The uncertainty of the variance can also be estimated by looking for more independent samples and making more variance estimates from those additional independtly collected samples and see how much the individual variance estimates differ. However, such luxury is hardly ever available.
The Jackknife (Quenouille, 1949) is a handy tool that can be used for different purposes. In statistics it is a resampling procedure (without replacement) to get better estimates of the reliability of parameters in many contexts, such as distribution parameters, or regression coefficients, etc.. The Bootsrap (Efron et al.,1986) is a resampling procedure with replacement for the same purpose, but uses a Monte Carlo procedure. So, in both methods the same sample is used many times but in different ways.
Moreover, if we are uncertain about the underlying distribution type, the Jackknife is a non-parametric approach to resampling the original sample, by taking sub-samples where one of the observations is excluded. Despite the "song and dance" we made elsewhere about iid violation in sampling, we consider the subsamples as independent. The aim is to find a "standard error" of the variance, but it could also be the standard deviation. The procedure for the standard deviation is as follows and illustrated with a sample of porosities:
From this sample we draw 9 subsamples of size 8, each time leaving out one of the porosities.
For each of these we calculate the sample mean and standard deviation, as well as the sample mean and standard deviation of the total sample. We get meanall = 10.8555555556 and stdevall =2.3130067012'.
The means and variances of the subsamples are given below:
Insted of one sample estimate of the mean and the standard deviation we have 9 such estimates, although not independent. If we consider them independent, we would take the mean of the 9 estimates for the parameter value. Not surprisingly, the mean of the subample means is equal to the original sample mean. But for the standard deviation it is 1.7443, slightly smaller than the
stdevall.
General considerations
Jackknife
No. 1 2 3 4 5 6 7 8 9
Sample size = n = 9
por. % 13.2 12.7 9.8 10.2 8.3 8.9 11.7 12.5 10.4
1 2 3 4 5 6 7 8 9
Mean 10.5625 10.6250 10.9875 10.9375 11.1750 11.1000 10.7500 10.6500 10.9125
Stdev 1.6141671891
1.715267576 1.8192914633 1.8492759201 1.5618212812 1.6953718513 1.83692289 1.7476514854 1.858907129
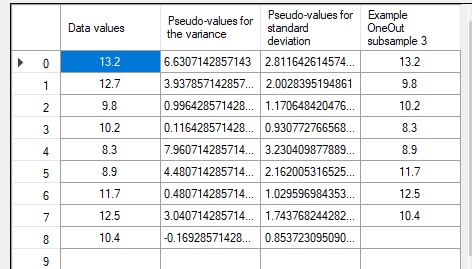
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ps Mean | 10.5625 | 10.6250 | 10.9875 | 10.9375 | 11.1750 | 11.1000 | 10.7500 | 10.6500 | 10.9125 |
| ps Stdev | 2.8116 | 2.0028 | 1.1706 | 0.9308 | 3.2304 | 2.1620 | 1.0296 | 1.7438 | 0.8537 |
Note that the pseudo values for the mean are the same as the original porosity values which were left out. This is always the case for the mean, so the mean of the pseudo values is the same as the meanall. The mean of the pseudo values for the standard deviation give the jackknifed estimate of the standard deviation as 1.7706, a bit larger than the estmate on the original sample. The standard error of the standard deviation is obtained in the same way as the standard error of the mean, i.e. dividing by the square root of n. This gives 0.2857. The parametric standard formula where the standard deviation is divided by the the square root of (2n) results in: 0.4118, substantially larger.
The results are shown below, together with the jackknife results in the upper table, as given by my program "jackBoot".
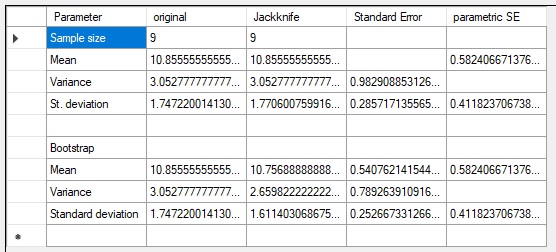
The upper part of the lower table refers to the jackknife results, the lower to the bootstrap.
The advantage of using the jackknife or the bootsrap appears to be, the resamples estimate of the parameter and the standard error, which can be quite different from the parametric equivalent, if available. Parameter estimates from a sample assuming a normal distribution could be unrealistic if the distribution is not well behaving or unknown.