Analysis of Variance
Generally the result of a resource assessment or prospect appraisal is an expectation curve, c.q. a distribution of possible volumes to be discovered as well as the chance to discover (POS). Such a distribution has a variance, often a considerably large one, demonstrated by the difference between, say the P90 and P10 percentiles.
The expectation curve, in the case of a appraisal system based on a multivariate technique, is the result of the interplay of a number of independent variables that resulted in the value of the dependent variable, i.e. the reserve estimate. It would be useful to have a way to estimate the individual contributions of the independent variables, which are the "sources of uncertainty" of the volume of hydrocarbons. Here we will discuss the uncertainty of the "unrisked expectation curve". The POS also contributes to the total uncertainty of the prospect and is explained statistically elsewhere.
Analysis of Variance is a technique to analyse the contribution a set of variables, in this case, in multiple, or multivariate regression. For instance HC charge is a function of a set of geochemical factors. The success of a multiple correlation in this situation is measured as the amount of variance in HC charge that is explained by the geochemical input variables. The variance of the expectation curve is split in two fractions: The part (fraction) of the total variance explained by the independent variables which is R-square, the coŽfficient of multiple correlation. So (1 - R2) is the part that is not explained by the input variables. The next step is to split the R-square part into the parts that correspond to the independent variables by using the results of the multiple regression. The relative contributions are proportional to the squared t-values in the multiple regression.
Various practical difficulties arise when trying to do this: the type of distribution of the independent ("input") variables is usually consisting of a set of zero values and the remainder a distribution of unspecified nature. This also holds for the dependent variable (the expectation curve). An estimate of the individual contributions in this non-ideal case is achieved by the following procedure:
- The vectors of the dependent and independent variables are changed into ranks, so that they all have comparable (rectangular) distributions, although with some loss of information.
- Multivariate regression of the recoverable HC type is made on the set of input variables, using Spearman's rank correlation (Kendall tau rank correlation might serve equally well). Roughly speaking, the expectation curve was the result of using a multiple regression equation. Here we measure the effect of an input variable of the appraisal model on the end result. If an input is not correlated at all to the end result, it can not contribute to the total explained variance.
- The individual contributions of the input groups is calculated from the t-test statistics. The t-value for a variable is the regression coŽfficient, divided by the standard deviation of this coŽfficient. The contributions of the variables are proportional to the squared t-values.
- The remaining, unexplained variance is contributed to the imperfections of the appraisal model. Theoretically, a perfect appraisal model exactly predicting reserves from geology would have a Rsquare of 1.00 (100%). The system I used based on world-wide calibration with a large learning set achieved 63%.
- An ANOVA table shows the sources of variance as percentages that should add up to 100% (of the explained variance). The same information can be displayed in a "tornado" diagram"
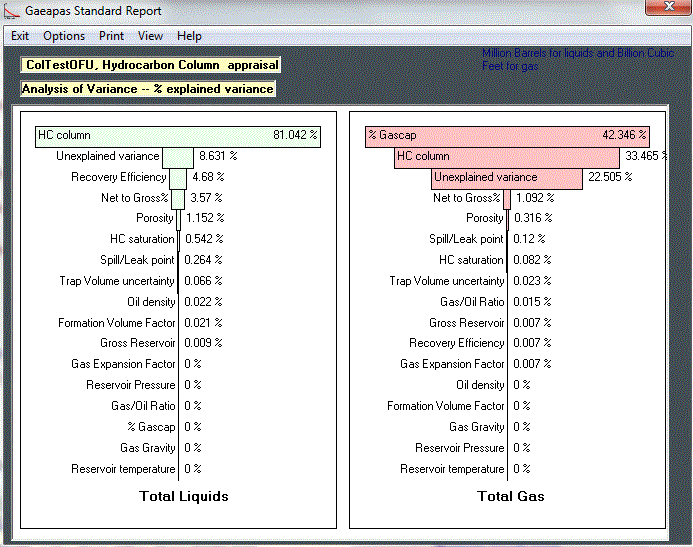
This example shows how difficult it would be to estimate the contribution of individual variables without the help of the ANOVA method. The example refers to a simple appraisal option in the Gaeapas program that asks for an estimate of the length of the hydrocarbon column and the percentage of that which is free gas. As shown, the two variables are overwhelmingly contributing to the total uncertainty.
ANOVA can suggest what kind of information would be worth having to reduce the uncertainty, i.e. risk. It also can help to estimate degrees of dependence amongst prospects, because dependence is about variance and how much variance prospects have in common, the "covariance".
In the case of an appraisal model that is based on subjective probabilities of a number of variables, such as are widely used in the industry, the ANOVA is solved in a different way.