Economics
- Overview
- Some basic principles
- Cashflow calculations
- Taxation
- Contract types
- Economic Cutoff estimation
- Expected Monetary Value (EMV)
- Group of prospects
- Summation of reserve estimates
- Decision trees
- Oil price, Gas price
- Pollution and theft
- Scenarios
- Forecasts
- Ranking of opportunities
Economic analysis is, in this context, the translation of barrels of recoverable oil or cubic feet of gas into dollar value. There is an interaction between the meaning of "recoverable" and economics, because secondary recovery is more costly than primary, not to speak of enhanced recovery. When we say "dollar value" we have to make clear whether we speak of real value (considering inflation) and/or present value (money in the future has normally less value than today). Oil and Gas prices obviously are most important amongst the various factors in the calculation. Unfortunately, such prices are quite unpredictable in the long term, such that calculations are often made for a number of oil price scenarios. To complicate matters further, the types of contract that govern the possible profits for a company are many, and history has shown painfully that a contract may not last till its specified end date, through a sudden re-negotiation or nationalization. These aspects will be highlighted in the following pages. You may also find the paper by Haldorsen (1996) useful as an introduction that covers most of the economic aspects of evaluation and decisionmaking. A more recent book that has been made available on the internet is by Kasriel & Wood (2013), which is specifically aimed at the Upstream.
Here are some definitions of the terms that are commonly used:
Some basic principles
Present Value
Present Value is used in order to compare the profitability of various projects for decision making. The concept of "present value" or "discounted money" is based on the reasoning that money earned at a certain moment may be re-invested at a certain amount of interest, or put into a savings account. If the profitability of the company is 15% on investments, it stands to reason to use this as a yardstick to compare profitability of projects. The percentage used is called "discount rate", "hurdle rate" or "cutoff rate". Discount rate is the more general term that is used in PV calculations and does not necessarily imply screening or acceptance of projects. The present value concept is widely used in economic evaluation of field development, but also to evaluate the cost of exploration programs. The idea is similar to that of RT money, except that the interest percentages used are usually larger and the result is labelled "PV".The PV calculations become very important if the phasing of capital expenditure is made over a number of years and when the positive cash flow out of production comes much later over a twenty or more years period. For instance, the PV value of $ 100.- in the year 2000 is only $ 32.69. This results from discounting the $ 100.- by 15% eight times for the eight years between the middle of the year 2000 and the middle of 1992.
The formula for calculating PV of an amount is given in its simplest form as:
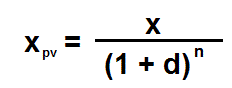
where X is the undiscounted amount in the future, d the discount rate (as a fraction) and n the number of years. This the "discrete" formula. It can be argued that money can be re-invested in the company continuously. Therefore, the above formula would not be entirely correct. The difference between annual and continuous discounting can best be explained by considering the growth of a capital sum X that is put in a savings account with annual interest 100i%. Then similar to the above formula the growth of capital on the annual basis is:
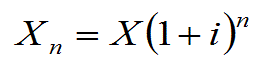
Now assume that the year is divided into m equal parts. The interest over the m-th part of the year is i/m. Hence:
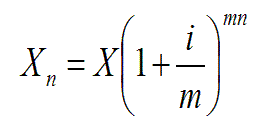
Capital growth on a continuous basis is derived by letting m increase to infinity:
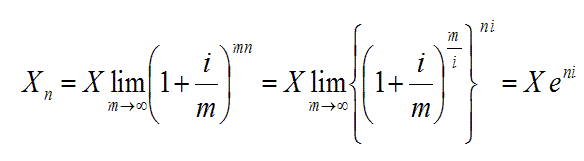
This calculation uses the mathematical fact that:

where e = 2.7183...
When discounting, the X is divided by exp(nd), switching back to "d" for discount rate instead of "i" for interest. The difference between the annual and continuous system can be significant: The PV value of 100$ at 15% discount is 49.72 with n = 5, the continuous discounted equivalent is 47.24. Computer programs for economic evaluation will usually use the continuous formula.
Cash Surplus
Cash Surplus is the result of a cashflow calculation, taking it to the end of the life of the field. If in Present Value and net of tax we can call it the PVNCS, a nice yardstick to compare opportunities and to estimate the Expected Monetary Value (EMV).
Pay-out Time
The pay-out time is the point in the cashflow curve where it crosses the zero line. In other words, how long is the expenditure more than the revenue, and in present value terms. The shorter the pay-out time the better.
Well initial
When a successful exploration well is tested the first indications are obtained about how prolific the discovery is. Some wells do not flow at all and have to be pumped straight from the beginning. That means high UTC (see above). At the other extreme there have been discoveries that produced over 100,000 b/d. In such case only few wells will drain a field. What is almost as important to know as the recoverable reserves is the "well initial" production rate, a stabilized sustainable production rate that can be used for the economic analysis. Each well will show a decline, depending on reservoir conditions. From the well initial and assumptions about speed and shape of decline the number of wells that are required to drain a field in an optimal way can be determined, apart from more complex reservoir engineering considerations. In turn this allows estimates of CAPEX to be made.
Well production is a function of the viscosity of the oil, the temperature of the reservoir, hence depth, the "drawdown", i.e. pressure differential between the formation and the borehole/tubing, permeability, and the "skin factor" a measure of the damage by drilling to the formation, that may reduce the inflow into the well. Translated into factors a geologist might be able to estimate for a prospect, we get the following proxies: API gravity, depth and porosity.