Evolution of
prospect appraisal methods
Assessments
are built of three ingredients—fundamentals, experience,
and judgment. In the early assessments,
judgment was the biggest factor. Today we are
relying more and more on experience. In the future
we will use all three but will be guided mostly
by the fundamental principles.
White and Gehman, 1979.
The most simple idea was to
provide a single number, as in "I believe there is a billion
barrels to be found there", not specifying any "degree
of belief". This is the subjective point estimate and we
would not consider this as "formal" prospect appraisal.
It is not entirely clear when formal prospect appraisal methods
were introduced in the industry. At least in the 1950ies,
mathematicians Croes and Baggelaar in R.D. Shell introduced the
concept of "expectation curves "to capture the
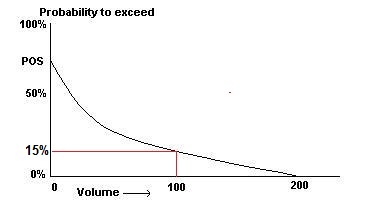
uncertainty of reserve volume estimates and chance of success. Expectation curves are
statistically speaking, the complement of the cumulative
distribution function (cdf) of a variable. They also used
mathematical techniques to combine different uncertainties.
Especially in Exploration, the expectation curve ("EC")
is useful, because the probability to have a zero outcome for a
variable can be clearly shown.
In the subjective reserve
distribution, there was a subjective chance of success and in the
case of success a (conditional) distribution of possible volumes.
Croes and Baggelaar used a histogram with 10 classes, the
frequency in each class estimated subjectively. Then an
expectation curve could easily be constructed on this basis.
Clearly, the geological/geophysical input to such a process was
rather ill-defined.
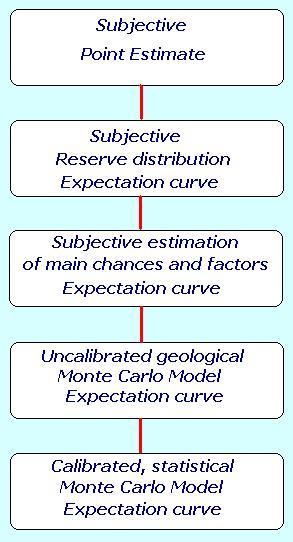
Then it was proposed to break the problem of estimation up into a number of independent parts, and "delphi" the parts. Combination then produced the EC, which was considered more reliable than estimating an EC directly.
With the increase of computer power, Monte Carlo simulation became fairly easy. The combination of factors could now be better and formally done, but the geological and especially geochemistry input was still meager, if present at all. In the last decades of the 20th century, great advances were made to quantify the process of generation and migration of hydrocarbons. This allowed the next step in the evolution: a proper "petroleum system model". This combined with the Monte Carlo method is what now is widely used in the industry.
More or less simultaneously, methods were developed that tried to reduce the dependence on subjective probabilities. Large databases with exploration data made it possible to use bayesian methods to refine chance estimates. A process of extracting prior distributions of input variables, then updating these to posterior probabilities made for more realistic and "calibrated statistical" expectation curves. In most assessment methods, a clear distinctiion is made between estimating the chance of success (POS) and estimating the volume of hydrocarbons in the success case.
With better and credible probability estimates, it becomes interesting to do an Analysis of Variance (ANOVA). Such analysis gives an insight in the sources of uncertainty. If a quantitative ANOVA is available, the addition or aggregation of reserve estimates can be made with a proper dependence estimate.
The expectation curve has found wide acceptance (SPE) and has been adopted by exploration as well as production.The figure below shows that the chance to find more than 100 volume units is 15%. Note that this chance is including the risk to find nothing. Nowadays reserve reporting should preferably include it, if not graphical, in percentile volumes, such as the P90, P50 and P10, but then the percentiles refer to the "unrisked" expectation curve. In addition the probability of success (POS) is given as well. In analogy with a lottery: the unrisked expection is the range of possible prizes and the POS is the probability to win a prize.