• Introduction
  • GAEA
  • About M.H.Nederlof
  • Publications
• Prospect appraisal
  • Overview
  • Aims of appraisal
  • Evolution
  • Petroleum System
  • Qualitative methods
  • Quantitative methods
• Resource Assessment
  • Overview
  • Fieldsize methods
  • PSA geological systems
  • Exploration Process Modeling
  • Logistic Models
  • Multivariate analysis
• Statistics
  • Probability
  • Distributions
  • Parameters
  • Monte Carlo methods
  • Calibration
  • Bayes theorem
  • Prior distributions
  • Update a normal distribution
  • Correlation/regression
  • Multivariate analysis
  • Analysis of Variance
  • Geostatistics
  • Monte Carlo
  • Addition of statistical distributions
• Economics
  • Overview
  • Principles
  • Cashflow
  • Taxation
  • Contracts
  • Cutoff volume
  • EMV
  • Prospect groups
  • Aggregation
  • Decision trees
  • Oil/Gas price
  • Scenario planning
  • Ranking
• Products
  • G50-structure
  • Gaeatools
  • Research
  • Consultancy
  • Contact
• Index, etc.
  • Index
  • References
  • Sitemap

Mean --- Definition

A number of observations can be described in full by giving the complete list, but also in a more condensed fashion by giving the arithmetic mean value, or shortly "mean". The mean is the sum of all the numerical observations divided by their number, the "sample mean". That could deviate considerably from the true mean of the whole population, depending on the sample size. It is expressed as:

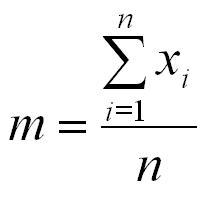
For a symmetrical distribution of the numbers this is a meaningful parameter. For a skew distribution observed for quite a few geological variables, it may be a bit misleading. Then other statistical parameters describing the "central tendency" of the observations are possibly better measures, such as the "most likely value": the mode.

If a sample is only small and the variation of the observations large the value of the estimated mean is not a very stable or reliable value. The accuracy of the estimated mean from a sample can also be estimated (see Variance).

Arithmetic means play an important role when the results of several individual appraisals have to be summed. In prospect appraisal (or gambling) the term used for the mean is "expectation". In a lottery there are a set of prizes and a number of lottery tickets. The value of a ticket is the sum of all prizes devided by the number of tickets. A dutch State lottery ticket costs 25 guilders, but the value, or expectation is only 16. So, in theory, you loose 9 guilders by buying a ticket. In prospect appraisal, we usually consider a possible prize: The MSV, and the chance to win it: POS. The Expectation of this uncertain situation is POS X MSV. Expectation is also called "Certainty Equivalent".

A few caveats:

• The P50 is the meam, not the MSV! The P50 is the median

  .

• A useful rule to remember: The expectation of the sum is the sum of the expectations.

• Note that sometimes the term "unrisked mean" is found in prospect appraisal reports. This refers to the mean of all non-zero values in the distribution (or MSV). Such unrisked means can not be added to get the unrisked mean of a number of prospects! The unrisked mean is a "conditional mean", based on the condition that the values must be positive (i.e. non-zero). Other conditional means are often used when values below a certain minimum have to be disregarded: Total Organic Carbon % when the minimum is set at 1.5 %. Similarly, the mean porosity of the net reservoir, when a cutoff porosity of e.g. 15% is used.

Home