Quantitative Appraisal Methods
for prospects
Having no good quantitative idea of uncertainty, there is an almost universal tendency for people to underestimate it. Thus, they overestimate the precision of their own knowledge and contribute to decisions that later become subject to unwelcome surprises.
E,C, Capen, 1976
Quantitative methods make a distinction between estimates of chances of success and volume estimates. Mostly, volume estimates are represented as a probability distribution, i.e. an expectation curve ("EC"), or its parameters. It is convenient to describe the conditional distribution of volume, conditional upon success. There is a good reason to do so, as, for instance, the mean (expectation) of the unconditional distribution comprises cases that are beforehand considered a failure. The economic calculations should not be based on such a mean value, but rather on the more realistic mean of the conditional distribution ("Mean Success Volume" or "MSV"). Any expectation of cash surplus has then afterwards to be discounted by the POS or Probability Of Success, also called "COS" (Chance Of Success).
There are a range of quantitative methods for prospects with varying degrees of geological sophistication. Before the advent of geochemical techniques, the size of a closure was the main parameter, and possibly a fill-factor, if there is doubt about the hydrocarbon charge or seal. Then the full petroleum system analysis ("PSA") came into use. The relatively simple PSA is using a number of chances of fulfillment, for which estimates must be given. The volume part is a trap-volume description, with a number of parameters that by the Monte Carlo method results in the conditional EC of hydrocarbon volume. All systems require a familiarity with statistical techniques. Although there are a multitude of textbooks available, I have discussed a selction of the relevant methods in a statistical techniques section. The following describes briefly a selection of quantitative appraisal methods that I have employed, developed or came across.
- Direct estimation of an expectation curve.
- Fieldsize distribution
- Petroleum System Analysis
- HC column or contact appraisals
- Material Balance
Direct estimation of an expectation curve
It would be possible to improve on a "point estimate" ( guessing a single number) by allowing uncertainty in the estimate. In statistics, one would think of giving not only the best estimate, but also some meassure of uncertainty, e.g. the standard deviation or the variance. But such a measure would imply that we also know the type of uncertainty distribution. is it normal, or lognormal, or still another shape?
To avoid this, one person, or a number of people could estimate a histogram by first agreeing on the number and size of histogram classes, and then deciding which weight to give to the histogram bars. We will call this here the "User-defined histogram"or " UDF". Such a procedure has sometimes been used to construct the expectation curve of the recoverable reserves in a prospect. If it is done in a committee it can be refined by the Delphi method for reaching a consensus.
But, as White and Gehman already argued in 1979, it is possibly better to break the estimation problem up into a number of factors and delphi the parts before reaching the final expectation curve. Such an approach implicitly assumes a model to combine the parts into an end result.
The UDF is one of the various methods to estimate input variables in more elaborate models. It has some advantages over a simple mean and standard deviation because even multimodal and irregular distributions can be represented this way.
Fieldsize distribution
In a mature province where a number of field reserves are available, a fieldsize distribution can be used to estimate the likelihood of a given size of future discovery. By assuming that the sample of fieldsizes is representative of future finds, we can use it as the expectation curve for a single undiscovered accumulation. It was Kaufman (1963) who argued that fieldsizes were following a lognormal distribution law. Many papers have been written discussing whether this is universally true, or that other types of distributions would fit the reported reserve data better. However, the lognormal is probably the most practical and best known way to represent fieldsize data in an oil province. Here is an example of a small sample of fieldsizes from the North Sea on a cumulative probability plot:
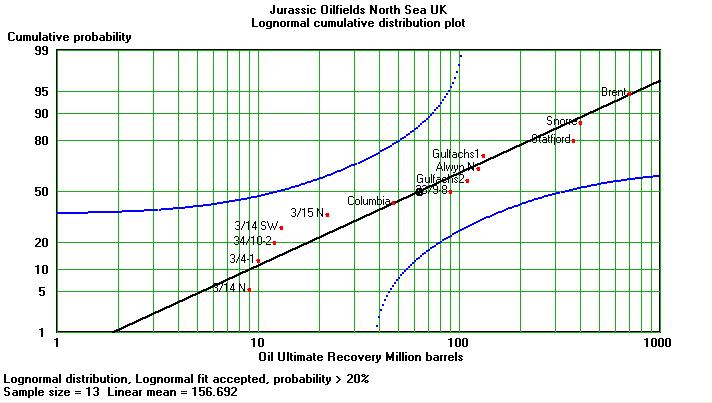
The horizontal axis is logarithmic, the vertical is a probability scale chosen such that points representing a true normal distribution will fall on a straight line. The straight line drawn here represents a lognormal distribution, because of the scale on the horizontal axis. The two curved lines are the "Kolmogorov-Smirnov" limits at 20%. This a severe test of goodness of fit. If one point falls outside these limits, the probability is greater than 20% that the sample does not come from a lognormal distribution. The 95% limits would be much further away from the straight line and outside the graph. The lognormality is hence accepted. To use this graph we make an important assumption: The future is the same as the past. This will not hold out during a long future, but, maybe for the next prospect it could be fair. In statistical terms this assumption is that the discovery process is a stationnary. Here we can read off that a new prospect with reserves like Brent would have only a 5% chance of being discovered. This does not take into account that we have a sample of only 13 fieldsizes so that the parameters of the lognormal distribution are not well establised. To refine estimates based on the graph, the parameter uncertainties have to be taken into account. To do this properly and at the same time create the expectation curve a Monte Carlo simulation is fairly easy to implement. It would sample at random from the uncertain lognormal distribution. The resulting expectation curve would be a vector of volumes sorted in ascending order.
This system is more often used for resource assessment, with various refinements.
This method recognizes that in a petroleum system a number of essential factors must be present and favourable. It is the most simple geological model for prospect appraisal and probably the most widely used system in the industry. The method makes a distinction between the modeling of the probability of (geological) success and the volumetric model.
The factors or "chances of fulfillment" are:
or variations of the above.
The probabilities are subjectively estimated, by one person, or as a consensus of several explorationists. The "final" (geological) probability of success (POSg) is calculated as the product of the five probabilities. This is statistically sound as long as the definitions of the individual chance factors are very clear and so defined that there is no overlap in the definitions. Otherwise there is dependence amongst the factors and the product will be misleading.
One of the problems with estimating the possible volume of hydrocarbons in the success case is exemplified by the porosity estimate. The unrisked volume is estimated as the product of a number of volumetric factors:
Petroleum System Analysis
Dependence could arise if the trap is a stratigraphic trap and basically formed by the presence of a seal. How do we think about trap existence if without a seal it would not be there? In such case we would assign a 100% chance for the trap and put any doubts about the combination trap/seal under the seal heading. in more complex cases logical errors are quite likely. Another problem is how the reservoir chance is established. Here we have a possible interaction with the description of the volumetrics. The reservoir quality description is a set of distributions for porosity, thickness, etc. which can themselves be described as having some risk, at least in combination. This particular risk must not be doubled in the reservoir chance factor. From these examples, it may be clear that the logic of the PSA is reasonable, but far from ideal, because of the lack of clarity in the probabilistic logic applied.
Another problem, (but not too serious) is that the chance factos are estimates, subject to uncertainty. A system that neglects this uncertainty produces biased POSg as a final product.
The volume in place then is given by the product:
What is meant to be estimated is the average porosity in the net reservoir. As the data available are usually a number of sidewall core porosities that include values that are not in the net reservoir, the data have to be culled to fit the description of "net", being above the "cutoff" porosity used to define "net reservoir". Then we have to calculate the mean of this truncated distribution and find the standard deviation. This would be the distribution of all the porosities in the net reservoir. The next step should be to divide this standard deviation by the square root of n (number of porosity data) to get the standard deviation of the mean porosity in the net reservoir (PHI). Note that, if the cutoff is 5%, an estimated mean PHI distribution should not include values less than 5%! (See also the discussion in the paper by Norman (2013).
In areas where the hydrocarbon charge to traps is more or less assured, but difficult to model with geochemical methods, it is practical to describe a trap, preferably in detail and in three dimensions. Then argue about how much of the trap capacity would be filled with oil and or gas. The methods are:
Hydrocarbon Column or Contact Appraisal
In the first method, the trap capacity can be considered as one big container and it is then dcifficult to limit the accumulation in a sophisticated way with lateral seal risk. In the latter two systems, a curve of trap volume from the culmination down to the last contact position is required, whic allows a proper interplay with a lateral seal risk function.
Material Balance
The material balance method includes the generation, migration, entrapment, retention and recovery volumetrically. The model may, or may not include the risks of fulfillment. In the Gaeapas system, the material balance includes the risks and is a calibrated system. Other systems include uncalibrated, subjective risk statements. The calibrated system depends on a substantive learning set of analogs and the multivariate analysis thereof.
In this more statistically underpinned process, the use of prior distributions for geological variables becomes useful. For instance, a global survey of porosity in relation to depth and maturity may provide a prior distribution that can then be defined with data from local analogs with bayesian logic.