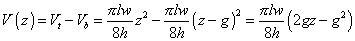Simple Geometric Trap models
Reserves calculations can be done by constructing first an "area/depth" graph of depth (Y-axis) versus Area (X-axis) and then integrating this curve to get the cumulative reservoir volume versus depth. If there is an analytical expression of the area/depth curve, also the volume/depth curve can usually be solved analytically. The area/depth graph has two curves: the top of the reservoir and the bottom. The behaviour of these curves is dependent on the folding style: similar, or parallel (parallel = concentric). The volume is contained in the reservoir between these curves. Therefore the volume below the top reservoir is found by integration and similarly that below the bottom. The reservoir volume follows then from the substraction of "bottom volume" from "top volume".
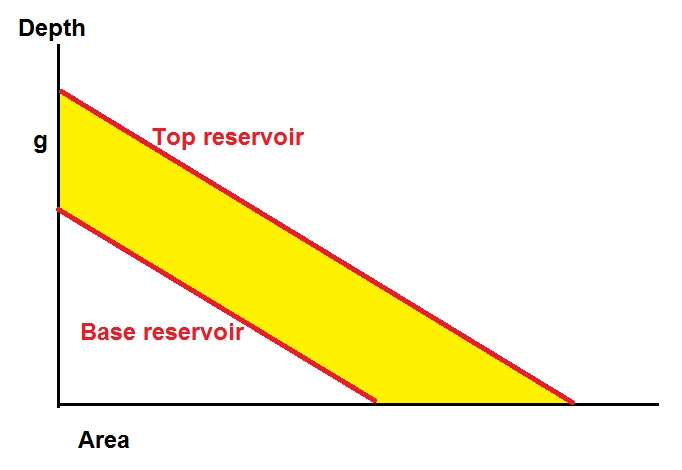
Here are a number of simple geometries with the derivation of volume where the thickness of the gross reservoir is "g".
Spherical model (Top segment of a sphere)
Parallel fold style
The above picture shows a cross section in the Length direction. The model is circular in this section, but as l and w may differ, the horizontal areas at various depths are usually ellipses. The axis of such an ellipse is "l" for length and "w" for width. In the cross section in the direction of l the radius Rl of the circle that describes the top reservoir is derived as:
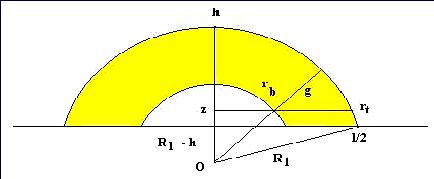
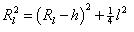
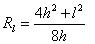
The areas at any depth z are the areas of an ellipse with two half axes rtl and rtw for the top reservoir and rbl and rbw for the base reservoir.
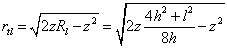
for the base, when z ≥ g:
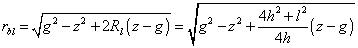
For both formulas h should be greater than 0. If h = 0 then the area is zero. Another less obvious constraint is that h should not exceed l or w. If that would be the case the structure would be more than a half sphere and the closed areas would increase from the top to a maximum area at h = l/2 and then decrease again. An extreme situation would be where h > l, i.e. more than an entire sphere! For a very steep structure, such as a pinnacle reef, the parabola model approximation is recommended.
Hence the area at depth z below culmination for the top reservoir is:
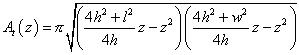
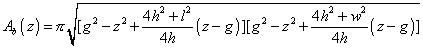
The above can be simplified considerably if we consider the form of the base not as an ellipse, but as a circle with the same area as the ellipse with axes l and w; then we can replace the squares of l and of w by lw. This results in:
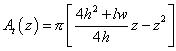
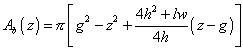
For the volume down to z we could integrate:
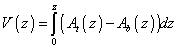
taking into account that Ab(z) = 0 for z ≤ g and that if g > h then g = h . The result by twice using the formula for the volume of a segment of the sphere and subtracting the volume below the base reservoir from the volume for the top reservoir gives the following formulas:
For the depth-below-culmination interval 0 to g:
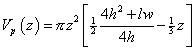
and for g to z, when z > g :
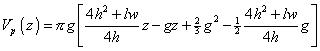
Similar fold style (Sphere)
In the case of a similar fold type the calculation is almost the same, but the radius of the base reservoir is then the same as the radius for the top. The results become:
For the depth-below-culmination interval 0 to g is the same as for the parallel type:
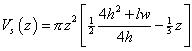
but for g to z, when z > g:
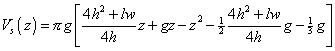
The cosine trap model (Sinesoidal wave form)
The cosine trap model assumes a structure in the shape of a sine wave. The spillpoints at either side of the trap are at -π and +π respectively. Because the cosine is chosen the culmination is at 0. The structure is steepest at mid-flank. The layers become horizontal at the spill-point. Any horizontal slice is in the shape of an ellips with diameters l and w. The vertical closure is h and corresponds to 2 if the level of the spillpoint is taken to be 0 elevation, i.e. the abscissa.
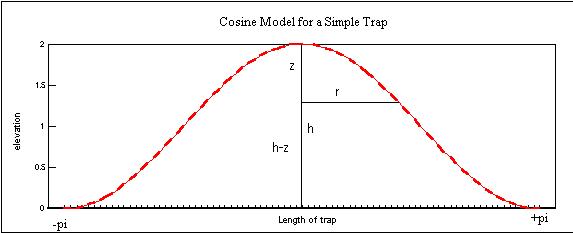
To calculate the volume at a depth z below the culmination, the radius r must be derived as a function of z.
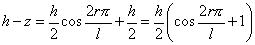
From this r can be solved as:

For the axis of the structure perpendicular to l the same formula applies. The area of the ellips at depth z below culmination therefore becomes:
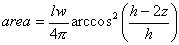
The volume down to the depth z is the sum of the cylinders with this area, replacing z by x, and thickness dx:
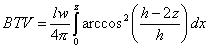
Using substitution:
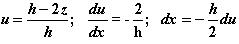
simplifies the integral to:
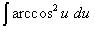
This indefinite integral is analytically solved as
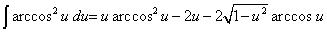
The volume down to z below culmination lies between u = 1 and u = (h-2z)/h and becomes:
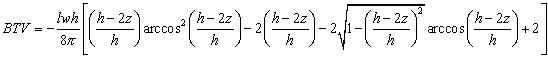
The above equation then provides the volume between the top reservoir and a horizontal plane at z below the culmination. To get the Bulk Reservoir Volume down to z, the volume below the base reservoir should be substracted. In the similar fold style this is calculated by taking (z-g) instead of z. In the parallel case no analytical solution was found. Hence the parallel case for the cosine trap uses the same algorithm to construct the base reservoir as used for the contoured structural trap.
A realistic anticlinal trap is likely to be somewhere in between the cosine and the segment models. This is because for many structures the spillpoints occur only in one cross section. Say, perpendicular to this no spillpoint is present. In such case, the dip becomes zero at the spillpoints in one section as given by the cosine, but in the other section at the spillpoint level the dip may be at a maximum as it is supposed to be in the spherical segment model. The result is an average of the two models being the best compromise.
Cylinder - ("Camembert cheese model")
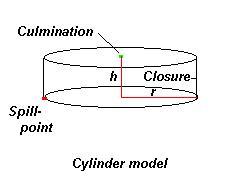
In this model the similar and parallel results are the same. The closure is equal to the thickness gross reservoir: h = g. To allow a noncircular area we have an equivalent radius:
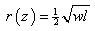
The area at z is
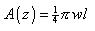
and the volume at z is
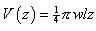
Monocline
For a monocline a separate calculation is made. For this model the Length (l), Width (w), Closure (h), and Gross reservoir thickness (g) are required. The length is supposed to be in the strike direction, the width is the horizontal projection of the slope. For the parallel case the situation is as follows:
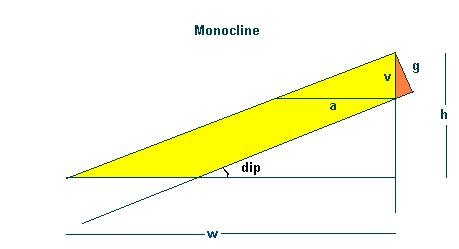
Note the orange area to the right of the vertical through the culmination. For Gaeapas this part is not included in the trap. Theoretically it might have to be included, if the updip truncation of the monocline is against a fault plane that is itself perpendicular to the dip of the monocline. However, this would involve another input variable that is not included in the Gaeapas program. In the contoured structural trap case there will be areas recorded that include the orange prism. In the simple trap version of the monocline this orange area/volume is not included.
In the figure
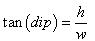
Down to a depth v below the culmination the width "a" increases:
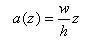
but below this level the horizontal line segment a is constant.
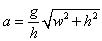
The depth v is greater than g:
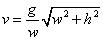
Volume down to z (z ≤ v) is
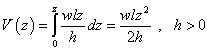
For v < z ≤ h volume down to z is
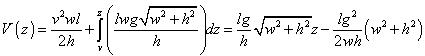
For the formulas above h and w should be > 0. The rather inelegant formula results from the requirement to use the standard input variables of Gaeapas for the calculation.
For the 'similar' monocline model the vertical interval called v above is now 'g'. The tan(dip) remains the same. This case gives simpler formulas for the volume down to depth z below culmination:
For 0 ≤ z ≤ g :
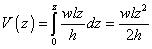
and for g < z ≤ h :
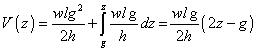
where h>0
The volumes for the similar style are again smaller than for the parallel case, as expected.
Parabola - (pinnacle reef model)
An inverted parabola y = x2 can be used as a model for a trap. This model does not limit the ratio h/(l/2) as is the case in the segment of the sphere model described above. The logic is as follows :
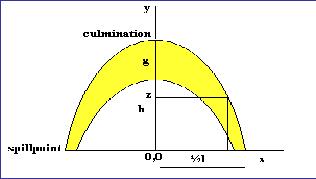
The formula for the parabola for the top reservoir is simply
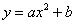
As the culmination is at a height h, this is also the value of b. Finding a is by getting the x value of the parabola where it hits the X-axis. The y = 0 and :
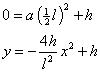
For the radius of the circle (c.q. half axis of the ellips in the length direction) at depth z below culmination x is solved from the parabola formula:
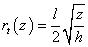
The area at depth z becomes:
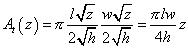
The volume below top reservoir down to depth z becomes:

The volume for the top reservoir can be used if g > h, i.e. the whole structure is filled with reservoir, as would be the case in a pinnacle reef. For steep folds the possibility must be included that g < h, so the volume below the base reservoir comes into play.
For the parallel fold model of the parabola it can be shown that a analytical solution does not exist. In that case we use the general algorithm to construct the base reservoir, such as in the contoured structural trap.
For the similar fold the base reservoir is the top moved down to g below the culmination. The volume below the base reservoir to be subtracted is the volume top reservoir at z-g:
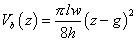
Hence the BRV down to z becomes For z < g :
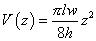
Note: quadratic increase with depth. and for z >= g: