Variance Definition
An "average" such as the mean, median or mode is a useful but insufficient description of a sample. The variation of numbers around the measure of central tendency is also very important. This spread, or dispersion can again be described by various statistical parameters. The most commonly used and useful measure is the "variance". It measures the degree of variation of individual observations with regard to the mean. It gives a weight to the larger deviations from the mean because it uses the squares of these deviations. A mathematical convenience of this is that the variance is always positive, as squares are always positive (or zero). It is defined as "the expectation of the squared deviations from the mean". The term was coined in 1918 by the famous Sir Ronald Fisher, who also introduced the analysis of variance. The variance is often denoted as "var" or, as the standard deviation (sigma) is the square root of the variance, "sigma-square":
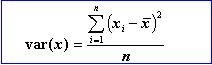
In the above formula the x with a bar on top is the mean of the observations. It has been found that in the case of a small sample a better estimate of the "population" variance can be obtained by dividing by (n-1) instead of by n.
The variance is a measure of uncertainty. As prospect appraisal tries to quantify the uncertainty of the hydrocarbon volumes that we hope to find, the variance is a fundamental concept that will appear in many of the discussions of appraisal and calibration methods. An interesting concept is "amount of information" H in a statistical sense. Some statisticians use the reciprocal of the variance V as such:
It is also called "precision", often used in bayesian statistics. In multivariate analysis the importance of geological variables for estimating probabilities of success and volumes is often judged on the basis of how much of the total variance they are able to explain, which is similar to how much information they represent.