Expectation of Exploration Cost (EEC)
Exploration decisions are based on the evaluation of possible profits against possible exploration and production expenditure and risk. If all expenditure is certain to be made, a simple calculation is sufficient. However, if the expenditure is made in phases where not all phases are necessarily carried out, a more sophisticated analysis of the expectation of expenditure is required. If this "option planning" element is overlooked, the normal evaluation procedures could turn out to be very pessimistic. The logic of the evaluation in the case of sequential exploration phases with decision points is explored here.
Calculation of Expected Monetary Value (EMV) requires an estimate of the exploration costs (EEC):
Where POS is the probability of success (fraction), the NCS the present value Net Cash Surplus in the case of success. Success is defined as finding more recoverable hydrocarbons than the economic minimum volume ("cutoff").
The failure case is represented in the formula by the complement of the POS, multiplied by the Expectation of PV exploration costs, or "EEC". Another expression for the second term in the above formula is "Expectation of exploration costs in the abortive case"
Exploration costs in the success case are normally included with the development costs in the Net Cash Surplus (NCS) because of fiscal reasons. Here EEC represents the exploration costs regardless of the fiscal treatment of such costs.
In the case of a single well to be drilled on a prospect, all that is required for the EEC is to PV the cost of drilling the well, if the well is not drilled immediately, but say, a year from now or even later.
However, even for a single prospect already defined by seismic work, the EEC may comprise more than the cost of the first well. This is because the EEC should be technically sufficient to reach the decision point where we decide that more than the economic cutoff volume has been proven, or abandon the prospect if less was found. Therefore the EEC may involve the drilling of one, two or more wells, depending on the complexity of the structure. This range of possibilities to "prove up the cutoff" could be expressed as "1.7" wells for instance, representing a judgement on what the average situation would be. If we consider decision points after each well, a more precise analysis can be made, as explained below.
We will now turn to more complex situations, where several investments are envisaged in a given timespan of several years, but with a number of decision points between these exploration phases. At the decision point the company can abort the venture. If such decision points do not exist, for instance because there is a fixed commitment to carry out all the work, regardless of intermediate results, we are back to the one well example, and only discounting is required for the expectation of the total exploration expenses.
Real Options
In exploration as well as in many other business contexts, the evaluation of an uncertain proposition is often done by the Expected Monetary Value based on the discounted cashflow model. If this is applied to a complex program in which decision points are present that allow flexibility in the investment, the discounted cashflow may overestimate the expected investments (e.g. exploration costs) if it is tacitly assumed that all phases will be carried out, regardless of the results along the way. As it seems, there are usually a number of "real options" that allow an explorer to quit at a decision point. Then some of the future investments are not only reduced by PV-ing them, but also by taking into account the uncertainty that the investment will really be made.
In the case of decision points, the procedure requires estimation the "conditional probability of continuation" (POC) after every phase of the exploration program, i.e. at the decision points. This involves imagining that at a given decision point we can choose to continue or quit, but that all previous phases have been done. This estimation is constrained by the results of the prospect appraisal. The probabilistic appraisal is assumed to specify a probability of success (POS) and a mean success volume (MSV) for the end result of the venture, regardless of when (meaning after which phase) it is aborted. To ensure consistency with the appraisal results, the cumulative product of the POC's must be monotone declining sequence that is always higher or equal to POS.
It may be that several phases are anyhow committed. Say, the first three phases are an obligation. Then the
Example (Deterministic demo)
To clarify the calculation of the EEC we take an example of a speculative frontier type exploration venture. The prospect evaluation resulted in a POS of 0.104. We envisage a five-year program in total, but we do not yet know whether there is a sedimentary basin in the concession area. So the first exploration phase is a $ 200,000 airmag survey. This first phase is assumed to have a 100% chance of being executed (year 0, phase 1) The other phases that might follow in case of encouragement are reconnaisance seismic (year 1, phase 2), then detail seismic (year 2, phase 3), followed by two stratigraphic test wells/structural tests (year 3, phase 4) and finally four wells on structures detailed by seismic (year 4, phase 5). The total six wells should be sufficient to decide whether the venture was successful (finding more than the "group" cutoff for the venture, which on average means the group MSV), or a failure (finding nothing, or a total volume of HC less than the group cutoff for the venture).
Note that there is an additional phase of expenditure in the case of success but that lies beyond the exploration campaign.
If we supply estimates of the POC's they may be based on the various risks that we included in the probabilistic evaluation of the venture. An example is the airmag survey of phase 1. The survey will hopefully answer the question of having a basin, deep enough for generation of HC. As the probability of HC charge has been estimated during the evaluation, it is clear that the POC for phase 2 must relate to the probability of the HC-charge. Also the probability of having traps must have been evaluated in the appraisal. This has a bearing on our estimate of the reconaissance seismic survey being encouraging.
We call the EEC calculation with a user-supplied set of POC's the deterministic method.
In the deterministic example the probabilities (POC's) were estimated to be as follows (Obligation phase number is 1).
| Expectation of Exploration Costs calculation | ||||||
|---|---|---|---|---|---|---|
| Phase number | 1 | 2 | 3 | 4 | 5 | (6) |
| Decision point | Airmag | Recon | Detail | 2 wells | 4 wells | (Produce) |
| Duration of phase (Months) | 12 | 12 | 12 | 12 | 12 | |
| Conditional POC | 1.000 | 0.650 | 0.500 | 0.800 | 0.500 | |
| Cumulative
Product of POC's = Probability of the exploration phase | 1.000 | 0.650 | 0.325 | 0.260 | 0.130 | 0.104 (POS) |
| Cost, $ 000' | 200 | 500 | 1,500 | 6,000 | 12,000 | |
| Cost PV15%, $ 000' | 185.549 | 414.515 | 1,153.690 | 4,281.312 | 7,943.918 | |
| EEC term | 185.549 | 269.434 | 562.424 | 1,669.711 | 1,549.064 | |
| Total PV0%. Full program | 20,200 | |||||
| Total PV15%. Full program | 13,978.98 | |||||
| EEC at PV15% | 4,236.18 |
So far so good. Now we estimate the costs of all the phases in "undiscounted" money. Then we discount each of these exploration expense items.
The next problem is to find the probabilities that are to be multiplied with each of these discounted expenses. There are a number of "exploration scenarios", as many as there are exploration phases.
The probability of execution of a phase is equal to the cumulative product of the POC's of previous phases including the current one (because POC's have been specified as "conditional probabilities").
The scenarios are:
| Exploration scenarios | |
|---|---|
| Airmag | 1.000 |
| Airmag + recon | 0.683 |
| Airmag + recon + detail | 0.471 |
| Airmag + recon + detail + 2 wells | 0.312 |
| Airmag + recon + detail + 2 wells + 4 wells | 0.210 |
| All phases turning to success (=POS) | 0.104 |
These probabilities are now multiplied with the PV costs of the phase to give the contribution to EEC. The total EEC is the sum of the EEC terms.
Note the enormous difference between the discounted full programme ($ 14 million) and the EEC ($ 4 million)!
The Monte Carlo approach (MC demo example).
Estimating the probability of continuation may be an unreasonable request. The subjective approach may also present a danger of working toward a minimum EEC, either subconsciously or on purpose, in order to "sell the venture".It may be better to allow for an uncertain input for the POC's. The most logical approach would be to let the POC's vary at random between 0 and 1, depicting ignorance about it. However, such a complete range between 0 and 1 is not possible under the constraint that the cumulative POC should never be less than POS. The first phase POC would remain equal to 1.000, but the others will vary within boundaries that honour the POS. Taking this into account a Monte Carlo analysis can be made to arrive at an EEC that makes minimal assumptions.
When we use the EEC program for this example we arrive at a mean value of $ 3 million instead of the more arbitrary subjective POC estimate. As a by-product we now have an expectation curve of the EEC:
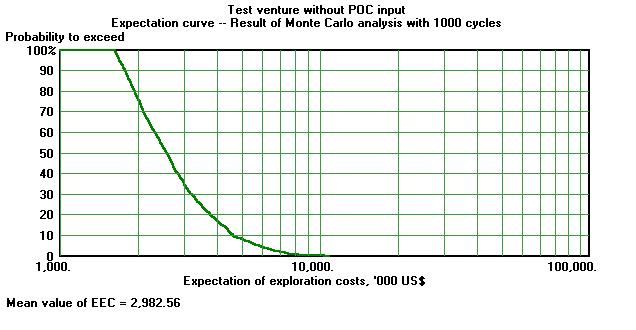
Or the histogram of EEC values:
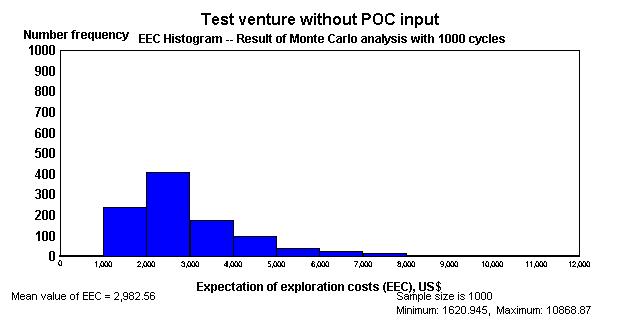
The vector of equally likely EEC values could be useful for an evaluation of the venture with a probabilistic EMV. Therefore the vector can be exported as a textfile.
The EMV of the venture
What about the whole venture? That is actually the final objective of the exercise. The calculation of EEC assumed that we would carry out phase 1 for certain. But having the whole evaluation and the EEC that can be used to calculate the EMV, we can evaluate the total venture. Despite the advantages of the option planning EEC calculated here, the EMV of the exploration venture may be too small to make it a viable proposition. In that case also the airmag phase would not be executed, i.e. the venture aborted.
A small computer program "EEC" is available to carry out the EEC calculations.