The Rectangular, or Uniform Distribution
In a rectangular distribution all values within a range between a and b are equally likely. The pdf (Probability Density Function) is a rectangle with surface equal to one.
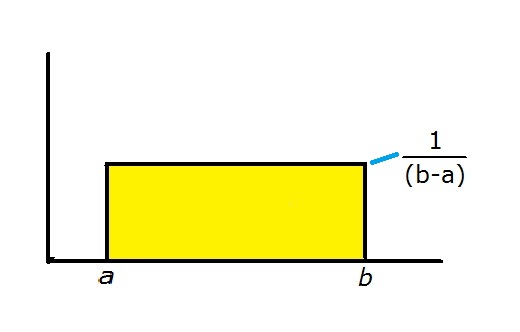
The cdf is a straight line from (a, 0) to (b, 1), being the integral of the rectangle.
The mean is:
The variance is:
The median is the same as the mean and the mode does not exist, as all values in the a to b range are equally likely.
The probability density is:
A rectangular distribution between 0 and 1 is easily generated by the RND (Random) function in programming languages and in spreadsheets. It is normally the workhorse for a Monte Carlo model, as many other types of distributions can be generated from the rectangular. An interesting example of such a process is generating a standard normal deviate by summing 12 uniform random numbers between 0 and 1. The sum of those has an expectation (mean) of 12 times 0.5 is 6. The variance is then 12 times (1-0)/12 which gives 1. If we subtract 6 from the sum of the 12 random numbers (the variance is not affected by this operation) we obtain a standard normal deviate with zero mean and variance of 1. It remains an approximation, but for a simple Monte carlo analysis acceptable.