Trap Description in the Gaeapas appraisal model
The basic requirement of the trap model is that the Gross Reservoir Volume (GRV) is described as a function of depth below the culmination of the trap. This function can be an empirical one in the case of a given set of contours (depths and areas) at the top of the reservoir, or an analytical solution which presumes a simple geometric model.
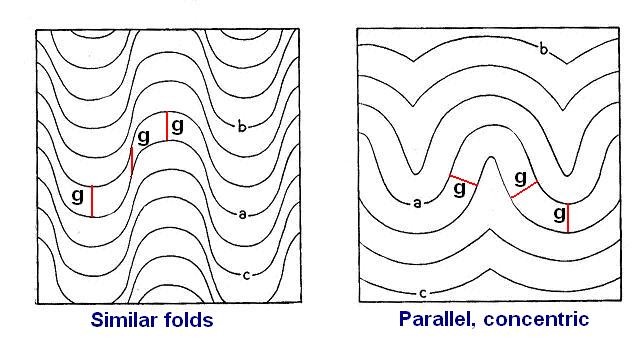
A further distinction is made between two styles of folding: Parallel or Similar. In the parallel model, the reservoir thickness (g) is constant when measured perpendicular to the top reservoir surface. In the Similar style, the reservoir thickness is constant in a vertical direction. Hence the Similar style uses a vertical translation downward of the top reservoir surface to get the bottom reservoir configuration. This ia a good enough approximation, if folding is gentle. However, if dips are some ten degrees or more, the Parallel style may be a better approximation. Then the base reservoir has to be constructed geometrically, with the usual problem of "lack of space" in the centre of an anticline, making the construction impossible occasionally. An example in Carboniferous limestone in the Belgian Ardennes shows how the lack of space is accomodated by a fault following the axial plane.

A special case for contoured traps is the stratigraphic trap. The input requires to give contours (depths and areas) of both top and bottom of reservoir. The stratigraphic trap requires description of, not only the top seal, but also of the bottom seal, as in a wedge, leakage is possible through the bottom of the reservoir. When several reservoirs in a single prospect are evaluated, it is important to distinguish two situations:
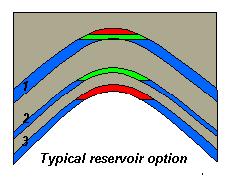 "Typical reservoirs" |
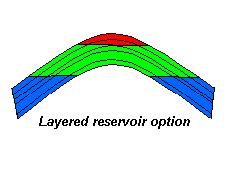 "Layered reservoir" |
In the case of the Typical reservoir, one description of the most common amongst a number of typical reservoirs suffices. The model uses that description and multiplies the volumes by the number of these reservoirs. That number is again a separate input as a discrete distribution of the number of reservoirs and requires also the total thickness between the top of the first and the bottom of the last typical reservoir. A rough approach, but practical in deltaic sequences.