Decision Trees
The simplest form of a decision tree for exploration is:
It will be clear that the decision tree is only valid if we have a choice: to drill or not to drill. If by the contract obligation we have to drill the well anyhow, the choice is not there, or there are negative consequences if we do not drill. To make the right choice, we must try to evaluate the consequences of each branch of the tree. So, in this example we may attach an expected value (PVNCS). The option not to drill may also have a positive value: we save money for another opportunity, which also will have a value. No wonder that a whole science has evolved around decision tree logic. A useful textbook is "Decision Analysis" by Howard Raiffa (1970), which also includes the Bayesian aspects.
A related tree structure is a "Chance Tree". This is not about decisions, but serves to clarify various possible outcomes in an uncertain situation:
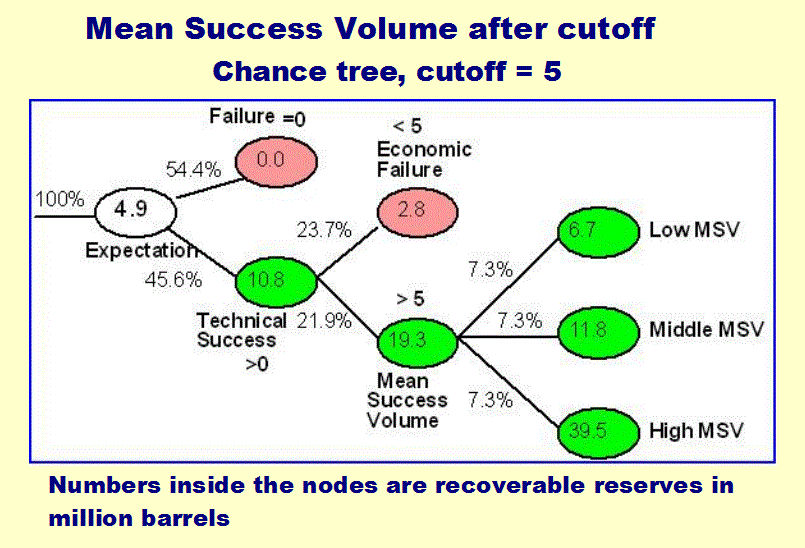
The chance tree allows us to summarize an expectation curve into a number of significant parts. The tree is entered with the assumption that we will drill the prospect (probability=100%). Then there are two branches; the geological POS = 45.6%. The dryhole has a probability of 100 - 45.6 = 54.4% with result 0. In the successful branch we have the Mean Success Volume before cutoff= 10.8. This branch is called "technical success". This, in turn, can be split into a "teaser", an uneconomic part (P=23.7% for 2.8, the mean for all values between 0 and cutoff 5) and an economic part (P = 21.9% for 19.3, the mean of all numbers between 5 and the maximum). Note that this 21.9% is the "economic POS".
For an evaluation, the Mean Success Volume after cutoff (19.3) may be too rough, so it is split into three equally likely parts: the Low, Middle and High success volume, each with a probability of 21.9/3 % = 7.3%.
Note that the expectation is less than the cutoff. If you do not understand this chance tree, you might be worried, but one should not compare the expectation with the cutoff! The cutoff lowered the geological POS of 45.6% down to 21.9%. That is where the cutoff hits the prospect. The cutoff is the minimum volume in the "unrisked" expectation curve. The mean of that curve is then the MSV, or Mean Success Volume.
In decision trees, a mixture of decision nodes and chance nodes will usually occur.
Option planning and Value of Information
An example of the Value of information shows the logic in an appraisal case. One well has been drilled and is a discovery. Do we drill an outstep well to get a better grip on the reserves, or can we build a production platform on the basis of the first well only? Similar problems of decision about getting more information are found in exploration programs. Do we spend more on seismic, or do we risk drilling on the basis of the present mapping? See the page on Expectation of Exploration Costs"